ㅅㅇ
머신러닝 _ 13_01 선형회귀 모델 개요 본문
머신러닝 _ 13_01 선형회귀
1. 선형회귀 개요
선형 회귀(線型回歸, Linear regression)는
종속 변수 y와 한 개 이상의 독립 변수X와의 선형 상관 관계를 모델링하는 회귀분석 기법.
2. 선형회귀 모델
- 입력 Feature에 가중치(Weight)를 곱하고 편향(bias)를 더해 예측 결과를 출력한다.
= > Weight와 bias가 학습대상 Parameter가 된다.
- 각 W들은 타켓을 예측하는데 각각의 feature가 어떤 영향을 주는 지를 뜻하게 된다.
- b는 모든 feature가 0일 때 예측값

3. 기본예제 : LinearRegression
- 가장 기본적인 선형 회귀 모델
- 데이터 전처리
선형회귀 모델사용시 아래와 같은 전처리를 해줘야 한다.
- 범주형 Feature
= > 원핫 인코딩
- 연속형 Feature
= > Feature Scaling을 통해서 각 컬럼들의 값의 단위를 맞춰준다.
= > StandardScaler를 사용할 때 성능이 더 잘나오는 경향이 있다.
# 기본 예제 Boston DataSet 보스톤의 지역별 집값 데이터셋 을 이용하여 선형 회귀 모델 분석을 해보자.
- MEDV= target, CHAS = 범주형 Feature (0또는1), 그 외 컬럼 모두 연속형 Feature
1) 데이터 불러오기 및 데이터프레임 만들기
import pandas as pd
import numpy as np
from sklearn.datasets import load_boston
boston = load_boston()
X, y = boston.data, boston.target
df = pd.DataFrame(X, columns=boston.feature_names) # 특성 feature-컬럼
df['MEDV'] = y # target
2) 선형회귀 모델 분석에서의 전처리
- CHAS Feature : 원핫인코딩
- X, y 분리, train/test set 나누기
- 연속형 : Feature scaling
# CHAS Feautre - 원핫 인코딩
df2 = pd.get_dummies(df, columns=['CHAS'])
# X, y 분리, train/test set 나누기
y = df2['MEDV']
X = df2.drop(columns='MEDV')
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
# Feature scaling
from sklearn.preprocessing import StandardScaler, MinMaxScaler
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
3) 선형회귀모델 평가지표 함수 생성
from sklearn.metrics import mean_squared_error, r2_score
def print_regression_metrics(y, pred, title=None):
mse = mean_squared_error(y, pred)
rmse = np.sqrt(mse)
r2 = r2_score(y, pred)
if title:
print(title)
print(f"MSE: {mse}, RMSE: {rmse}, R2: {r2}")
print("-"*100)
4) 모델 생성 및 학습
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(X_train_scaled, y_train)
5) 학습 대상 Parameter : Weight 와 bias
- 입력 Feature에 가중치(Weight)를 곱하고 편향(bias)를 더해 예측 결과를 출력한다.
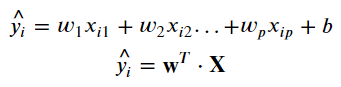
- .coef_ : W1 ~ Wp 을 담은 array 로 반환
- 각 W들은 타켓을 예측하는데 각각의 feature가 어떤 영향을 주는 지를 뜻하게 된다.
- .intercept_ : b 를 반환
- b는 모든 feature가 0일 때 예측값
lr.coef_array([-0.97100092, 1.04667838, -0.04044753, -1.80876877, 2.60991991,
-0.19823317, -3.00216551, 2.08021582, -1.93289037, -2.15743759,
0.75199122, -3.59027047, -0.29704388, 0.29704388])
lr.intercept_22.608707124010557
5) Coeficient 의 부호 = > Feature 의 중요도 ( 각 feature 별 weight = .coef_ )
- weight 의 부호 ---- y = w * X ( = 각 weight * 각 Feature 값) + b
- 양수: Feature가 1 증가할때 y(집값)도 weight만큼 증가한다.
- 음수: Feature가 1 증가할때 y(집값)도 weight만큼 감소한다.
- 절대값 기준으로 0에 가까울 수록 집값에 영향을 주지 않고 크면 클수록(0에서 멀어질 수록) 집값에 영향을 많이 주는 Feature 란 의미가 된다.
pd.Series(lr.coef_, index=X_train.columns)CRIM -0.971001
ZN 1.046678
INDUS -0.040448
NOX -1.808769
RM 2.609920
AGE -0.198233
DIS -3.002166
RAD 2.080216
TAX -1.932890
PTRATIO -2.157438
B 0.751991
LSTAT -3.590270
CHAS_0.0 -0.297044
CHAS_1.0 0.297044
dtype: float64
6) 예측 및 평가
pred_train = lr.predict(X_train_scaled)
pred_test = lr.predict(X_test_scaled)
# 위에서 만든 선형회귀모델 평가지표 함수 - (정답, 예측, title)
print_regression_metrics(y_train, pred_train, title='LinearRegressor: Train')
print_regression_metrics(y_test, pred_test, title="LinearRegressor: Test")
# 반환 - MSE , RMSE, R2LinearRegressor: Train
MSE: 19.640519427908046, RMSE: 4.4317625644779355, R2: 0.7697699488741149
----------------------------------------------------------------------------------------------------
LinearRegressor: Test
MSE: 29.782245092302407, RMSE: 5.457311159564059, R2: 0.6354638433202124
----------------------------------------------------------------------------------------------------
7) 정답 y_test 와 예측 pred_test 시각화 비교
import matplotlib.pyplot as plt
plt.figure(figsize=(15, 7))
plt.plot(range(len(y_test)), y_test, label='MEDV', marker='x')
plt.plot(range(len(y_test)), pred_test, label='Pred', marker='o')
plt.legend()
plt.show()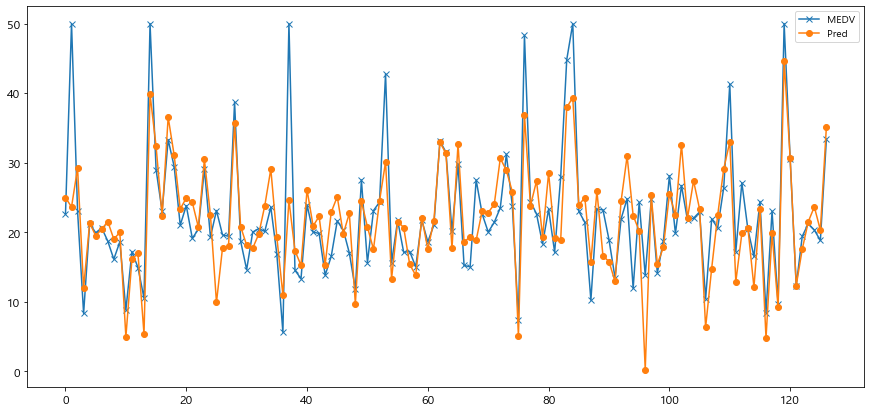
'AI_STUDY > 머신러닝' 카테고리의 다른 글
| 머신러닝 _ 14_최적화 _ 경사하강법 (0) | 2022.07.14 |
|---|---|
| 머신러닝 _ 13_02 선형회귀 _ 다항회귀 (0) | 2022.07.14 |
| 머신러닝 _ 12_회귀모델개요_평가지표 (0) | 2022.07.14 |
| 머신러닝 _ 08_지도학습_SVM (0) | 2022.07.14 |
| 머신러닝 _ 07_ 지도학습 _ 최근접이웃 (0) | 2022.07.10 |




