ㅅㅇ
머신러닝 _ 14_최적화 _ 경사하강법 본문
머신러닝 _ 14_최적화 _ 경사하강법
1. 최적화 (Optimize)
= > ' 학습 '에서 모델의 예측한 결과 값과 실제 정답 값의 차이 -- > ' 오차를 계산하는 함수 ' 손실함수 를 만들고
그 오차값이 최소가 되는 지점 그때의 Parameter 를 찾는 작업을 한다.
2. 최적화 문제
- 선형회귀 모델에서 오차는 w 에 영향을 받는데, 둘은 관계가 있는 것이다.
- 오차 구하는 함수 f(w) 의 값을 최소화(또는 최대화) 하는 arg 변수 w(파라미터)를 찾는 것.

- 예시 그래프 (설명을 위해 우리가 만든 손실함수 f(w) _ 원래는 우리가 만드는게 아니라, 모델이 학습하여 만드는 함수)
아래 그래프와 같이 weigth 에 따라 loss 오차 값이 달라지는데,
오차가 최소화 되는 arg 변수 w 파라미터를 찾아야 한다. = > 아래 그래프에서는 빨간점 (찾을 지점) 이다.

3. 목적함수(Object Function), 손실함수(Loss Function),
비용함수(Cost Function), 오차함수(Error Function)
- 손실 함수 loss function, 비용 함수 cost function 이라는 용어를 가장 많이 씀.
- 모델의 예측한 값과 실제값 사이의 차이를 정의하는 함수로 모델이 학습할 때 사용된다.
- 이 함수의 반환값(Loss)을 최소화 하는 파라미터을 찾는 것이 최적화의 목적
- 해결하려는 문제에 맞춰 Loss 함수를 정의한다.
- Classification(분류)의 경우 cross entropy를 사용한다.
- Regression(회귀)의 경우 MSE(Mean Squared Error)를 사용한다.
- 같은 계산 함수를 쓰는 것뿐이지, 평가함수 MSE과 동일하게 보면 안됨.
4. 최적화 문제를 해결하는 방법
1) Loss 함수 최적화 함수를 찾는다.
- Loss를 최소화하는 weight들을 찾는 함수(공식)을 찾는다.
- Feature와 sample 수가 많아 질수록 계산량이 급증한다.
- 최적화 함수가 없는 Loss함수도 있다.
2) 경사하강법 (Gradient Descent)
- 값을 조금씩 조금씩 조정해나가면서 최소값을 찾는다.
5. 경사하강법 (Gradient Descent)
- 다양한 종류의 문제에서 최적의 해법을 찾을 수 있는 '일반적인 최적화 알고리즘'
- 손실함수를 최소화하는 파라미터를 찾기위해 반복해서 조정해 나간다.
1) w 초기값을 랜덤하게 정해 loss 를 구한다.
2) 파라미터 벡터 W 에 대해 미분을 통해 손실함수의 현재 gradient(경사,기울기, 순간변화율)를 계산한다.
3) gradient 의 크기 가 감소하는 방향 (0 이 되는)으로 다음 벡터 W를 조정하여 loss 를 구한다.
- gradient가 양수이면 loss와 weight가 비례관계란 의미이므로 loss를 더 작게 하려면 weight가 작아져야 한다.
- gradient가 음수이면 loss와 weight가 반비례관계란 의미이므로 loss를 더 작게 하려면 weight가 커져야 한다.
4) gradient가 0이 될때 까지 반복한다. 그때의 w 값이 최적화된 파라미터
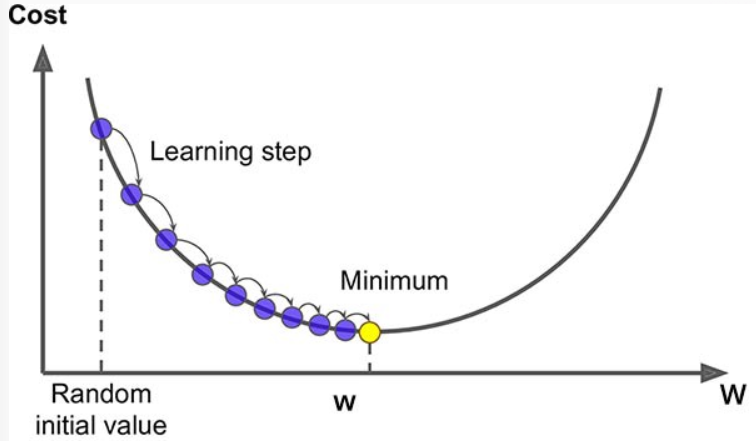
5.1 경사하강법의 파라미터

- 위 식을 통해 다음 W 값을 결정한다. W = W - α
- 미분한 값을 그냥 빼기에 너무 클 수 있어 이를 학습률로 조정한다.
- 하이퍼 파라미터 : 학습률 (Learning rate)
- 기울기에 따라 이동할 step의 크기. 경사하강법 알고리즘에서 지정해야하는 하이퍼 파라미터이다. (0 ~ 1 사이 실수)
- 학습률을 너무 작게 잡으면
최소값에 수렴하기 위해 많은 반복을 진행해야해 시간이 오래걸린다.
- 학습률을 너무 크게 잡으면
왔다 갔다 하다가 오히려 더 큰 값으로 발산하여 최소값에 수렴하지 못하게 된다.
5.2 예제
# 예제는 최적화 작업의 개념을 설명하기 위해 우리가 직접 loss 함수를 만들고 도함수를 구하여 시각화 한 것뿐이다.
실제로 이 일은 데이터를 가지고 머신러닝 모델이 하는 일. 설명을 위한 코드이지, 머신러닝 작업이 아님.
1) loss funtion 과 graident 를 구하는 loss 함수의 도함수 만들어주기
# loss 함수
def loss(weight):
return (weight-1)**2 + 2
# loss 함수의 도함수 - 각 weight에 대한 graident 를 계산해줌.
def derived_loss(weight):
return 2*(weight-1)
2) loss function 과 최적의 weight (gradient = 0) 을 찾는 연산 및 결과를 시각화
- 학습율 파라미터 설정
learning_rate = 0.4
learning_rate = 0.01
learning_rate = 1.1
- weight 설정
초기값 = 0 : 이 값 또한 원래는 머신러닝에서 random 하게 결정한다. 지금은 우리가 지정해준 것.
[ 코드 설명 ]
- loss function 그리기 (weight 에 따른 loss 값)
- 초기값 w = 0 일 때의 loss 값 마킹, w = 0 일 때 기울기 line plot
- 다음 weight 연산하여 결정. w = w - learning_rate * derived_loss(w)
- 아래 그래프는 위 과정을 6차 시도까지 반복하여 시각화 결과 보기.
- 학습율 파라미터를 조정해보며 결과 차이 보기
weights = np.linspace(-3,4, 100) # weights 후보들
plt.figure(figsize=(20,10))
# 손실함수 - weight에 따른 loss(손실, 오차) 값을 line plot으로 시각화
plt.plot(weights, loss(weights), 'k-')
# 학습율 설정 - weight지점에서 미분한 값에 곱해줄 값
learning_rate = 0.4
# learning_rate = 0.01
# learning_rate = 1.1
# 시작 weight (random inital value)
w = 0
plt.plot(w, loss(w), 'go', markersize=10) # w가 0일 때 loss 값에 마킹 (g:green, o:마커모양)
plt.text(w+0.1, loss(w)+0.1, '1차시도')
plt.plot(weights, derived_loss(w)*(weights) + loss(w), 'g--') # w=0 일 때 기울기(gradient, 미분값)를 line plot으로 시각화
print('1차시도: w={:.2f}, 기울기 = {:.2f}'.format(w, derived_loss(w)))
# 다음 weight를 결정하는 연산
w = w - learning_rate*derived_loss(w)
plt.plot(w, loss(w), 'ro', markersize=10)
plt.text(w+0.1, loss(w)+0.1, '2차시도')
plt.plot(weights, derived_loss(w)*(weights-w) + loss(w), 'r--') # red --선
print('2차시도: w={:.2f}, 기울기 = {:.2f}'.format(w, derived_loss(w)))
w = w - learning_rate*derived_loss(w)
plt.plot(w, loss(w), 'bo', markersize=10)
plt.text(w+0.1, loss(w)+0.1, '3차시도')
plt.plot(weights, derived_loss(w)*(weights-w) + loss(w), 'b--')
print('3차시도: w={:.2f}, 기울기 = {:.2f}'.format(w, derived_loss(w)))
w = w - learning_rate*derived_loss(w)
plt.plot(w, loss(w), 'mo', markersize=10)
plt.text(w+0.1, loss(w)+0.1, '4차시도')
plt.plot(weights, derived_loss(w)*(weights-w) + loss(w), 'm--')
print('4차시도: w={:.2f}, 기울기 = {:.2f}'.format(w, derived_loss(w)))
w = w - learning_rate*derived_loss(w)
plt.plot(w, loss(w), 'co', markersize=10)
plt.text(w+0.1, loss(w)+0.1, '5차시도')
plt.plot(weights, derived_loss(w)*(weights-w) + loss(w), 'c--')
print('5차시도: w={:.2f}, 기울기 = {:.2f}'.format(w, derived_loss(w)))
w = w - learning_rate*derived_loss(w)
plt.plot(w, loss(w), 'yo', markersize=10, alpha=0.5)
plt.text(w+0.1, loss(w)+0.1, '6차시도')
plt.plot(weights, derived_loss(w)*(weights-w) + loss(w), 'y--')
print('6차시도: w={:.2f}, 기울기 = {:.2f}'.format(w, derived_loss(w)))
plt.ylim(0,15)
plt.xlim(-4,5)
plt.xlabel('W')
plt.ylabel('Cost')
plt.grid(True)
plt.show()
- learning_rate = 0.4 일 때
= > w = 1 : 최적의 weight. (gradient = 0 이 되는 지점)
= > 초기 w = 0 일 때 부터 경사하강법을 통해 기울기를 줄여가며 기울기가 0 인 w 값을 구하였다.
이 값이 오차를 최소로 만드는 weight 값이다. -- > 이 작업을 머신러닝 모델 학습에서 이뤄진다.
1차시도: w=0.00, 기울기 = -2.00
2차시도: w=0.80, 기울기 = -0.40
3차시도: w=0.96, 기울기 = -0.08
4차시도: w=0.99, 기울기 = -0.02
5차시도: w=1.00, 기울기 = -0.00
6차시도: w=1.00, 기울기 = -0.00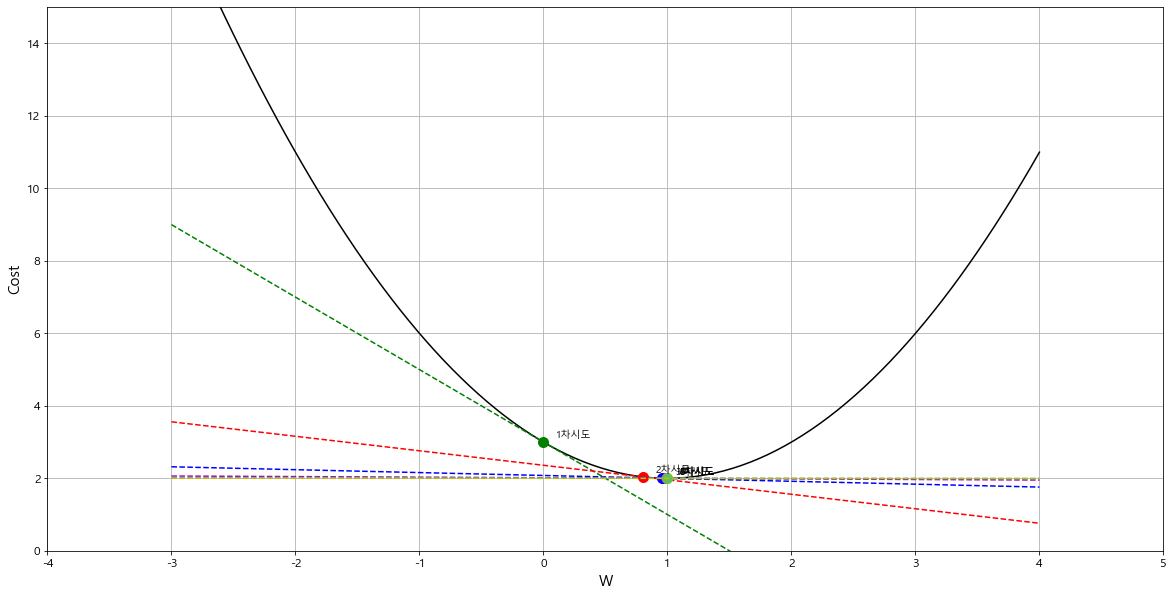
- learning_rate = 0.01 일 때 = > 너무 작게 잡음. 6차 시도 만에 찾지 못했다.
1차시도: w=0.00, 기울기 = -2.00
2차시도: w=0.02, 기울기 = -1.96
3차시도: w=0.04, 기울기 = -1.92
4차시도: w=0.06, 기울기 = -1.88
5차시도: w=0.08, 기울기 = -1.84
6차시도: w=0.10, 기울기 = -1.81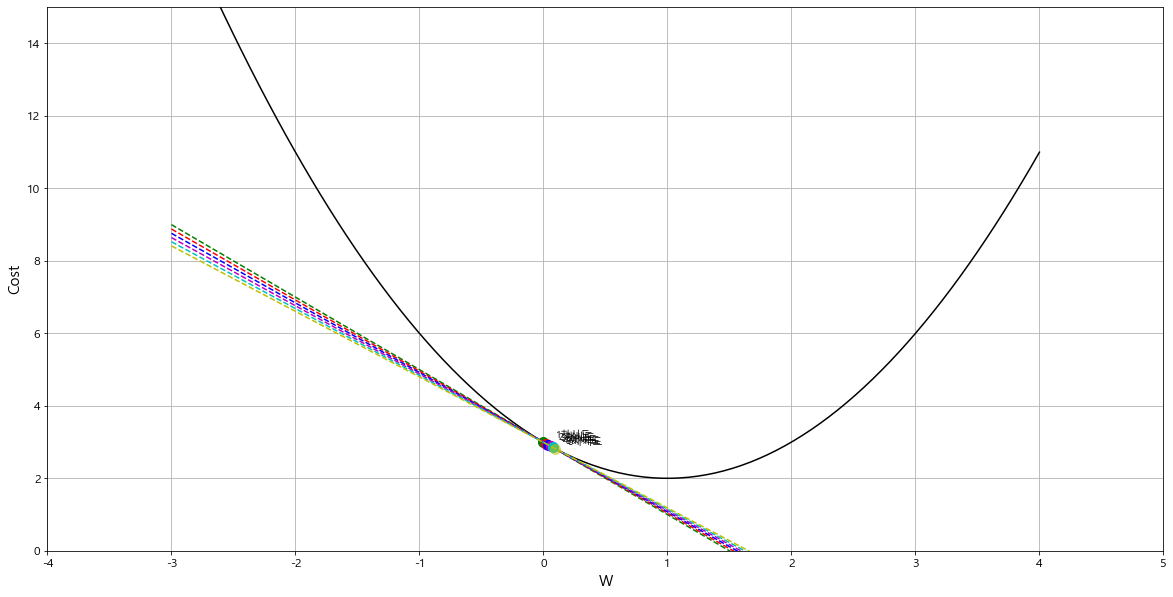
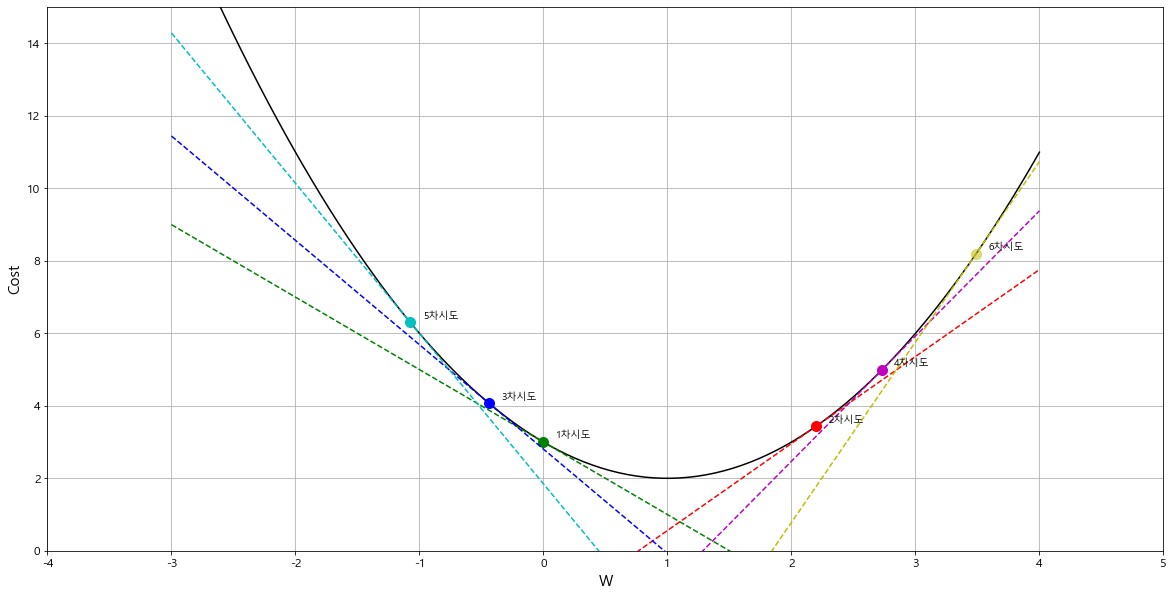
- learning_rate = 0.4 일 때 = > 너무 크게 잡음.
왔다 갔다 하다가 오히려 더 큰 값으로 발산하여 최소값에 수렴하지 못하게 된다.
1차시도: w=0.00, 기울기 = -2.00
2차시도: w=2.20, 기울기 = 2.40
3차시도: w=-0.44, 기울기 = -2.88
4차시도: w=2.73, 기울기 = 3.46
5차시도: w=-1.07, 기울기 = -4.15
6차시도: w=3.49, 기울기 = 4.98
5.3 반복문을 이용해 gradient가 0이 되는 지점의 weight 찾기
# 5.2 예제를 반복문을 통해 구현 (여기서는 초기 weight 값을 랜덤하게 지정함.)
w = np.random.randint(-3,3) # 초기 weight를 랜덤하게 선택 (-3 ~ (3-1)사이의 정수)
learning_rate = 0.4
# learning_rate = 0.001
# learning_rate = 10
max_iter = 100 # 최대 반복횟수(최적의 weight 를 찾으면 멈추고 못찾으면 최대 100번까지만 찾아본다.) 시간이 얼마나 걸릴지 모르니
w_list = [w] # weight 값들을 저장할 리스트
cnt = 0 # 몇 번 반복했는지 저장할 변수
while True:
if derived_loss(w)==0: # 기울기가 0이 되면 멈춘다.
break
if cnt==max_iter: # 반복횟수가 max_iter와 같으면 멈춘다.
break
w = w - learning_rate*derived_loss(w) # 새로운 weight 를 계산
w_list.append(w) # 새로운 wieght를 리스트에 추가
cnt += 1 # 반복횟수 1 증가
- 24 번 반복 끝에 찾음.
print('반복횟수:', cnt)
- 지정되었던 weight 값들을 저장한 리스트
= > 가장 마지막 값 1.0 이 최적의 weight 값이다.
w_list
[-1,
0.6000000000000001,
0.92,
0.984,
0.9968,
0.99936,
0.999872,
0.9999744,
0.99999488,
0.999998976,
0.9999997952,
0.99999995904,
0.999999991808,
0.9999999983616,
0.99999999967232,
0.999999999934464,
0.9999999999868928,
0.9999999999973785,
0.9999999999994758,
0.9999999999998952,
0.999999999999979,
0.9999999999999958,
0.9999999999999991,
0.9999999999999998,
1.0]'AI_STUDY > 머신러닝' 카테고리의 다른 글
| 머신러닝 _ 15_로지스틱 회귀 (0) | 2022.07.14 |
|---|---|
| 머신러닝 _ 13_02 선형회귀 _ 다항회귀 (0) | 2022.07.14 |
| 머신러닝 _ 13_01 선형회귀 모델 개요 (0) | 2022.07.14 |
| 머신러닝 _ 12_회귀모델개요_평가지표 (0) | 2022.07.14 |
| 머신러닝 _ 08_지도학습_SVM (0) | 2022.07.14 |




