ㅅㅇ
머신러닝 _ 12_회귀모델개요_평가지표 본문
머신러닝 _ 12_회귀모델개요_평가지표
1. 회귀(Regression) 이란?
예측할 값(Target)이 연속형(continuous) 데이터(float)인 지도 학습(Supervised Learning).
X 를 이용해 y 를 예측하는 모델.
선형회귀는 확보한 데이털를 이용해서, 두 변수 사이의 관계를 모델링하여 둘의 관계를 선형식으로 추정한다.
회귀 문제는 실제 식을 찾는 것은 불가능하며, 샘플을 이용해 실제 식을 추정한다.
- LinearRegression 모델이 학습해서 찾는 파라미터 제공 attribute
: 계수(coef, 가중치-weigth) 와 절편(intercept, 편향-bias) 를 통해 X과 y에 미치는 영향을 알 수 있기에
선형 회귀 모델은 학습에서 오차의 제곱 값이 최소가 되는 이 파라미터들을 찾아 선형 함수 직선을 만드는 것이다.
- coef_: Feature에 곱하는 가중치 (직선 방정식의 기울기)
- intercept_: 모든 Feature가 0일때 예측값 (직선 방정식의 y절편)
2. 회귀의 주요 평가 지표
1) MSE (Mean Squared Error)
- 실제 값과 예측값의 차를 제곱해 평균 낸 것 (제곱인 이유 오차는 +,- 값으로 서로 상쇄가 일어날 수 있기에)
- 실제 값에서 예측값을 빼야 오차가 된다.
- 오차는 +,- 값으로 더할 때, 서로 상쇄가 일어날 수 있다. 각 오차가 음수를 가지지 않도록 제곱해준다.
- 오차를 모든 예측값에 대해 구해야 하므로, 시그마를 취해 모두 더해준다.
- 오차의 전반적인 분포 확인을 위해 평균을 구해야 한다.
- 이상치가 존재하면 수치가 많이 늘어나며, 오차에 제곱을 하기에 오차가 크면 그에 따른 가중치가 높게 반영된다.
- scikit-learn 평가함수: mean_squared_error(y정답, pred예측)
from sklearn.metrics import mean_squared_error
mean_squared_error(y_test, y_pred)
- 교차검증시 지정할 문자열: scoring= 'neg_mean_squared_error'

2) RMSE (Root Mean Squared Error)
- MSE는 오차의 제곱한 값이므로 실제 오차의 평균보다 큰 값이 나온다. MSE의 제곱근이 RMSE이다.
- 에러에 따른 손실이 기하급수적으로 올라가는 상황에서 쓰기 적합
- mean_squared_error() 의 squared=False로 설정해서 계산. 또는 MSE를 구한 뒤 np.sqrt()로 제곱근을 구한다.
from sklearn.metrics import mean_squared_error
MSE = mean_squared_error(y_test, y_pred)
np.sqrt(MSE)
- 교차검증시 지정할 문자열: scoring= 'neg_root_mean_squared_error'
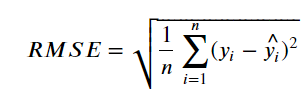
3) R square, 결정계수
- 평균으로 예측했을 때 오차(총오차) 보다 모델을 사용했을 때 얼마 만큼 더 좋은 성능을 내는지를 비율로 나타낸 값.
- 실제 관측값의 분산대비 예측값의 분산을 계산하여 데이터 예측의 정확도 성능을 측정하는 지표
- 0 ~1 까지의 수로 나타내어진다. 1에 가까울 수록 좋은 모델.
- scikit-learn 평가함수: r2_score(y정답, pred예측)
from sklearn.metrics import r2_score
r2_score(y_test, y_pred)
- 교차검증시 지정할 문자열 : scoring = 'r2'
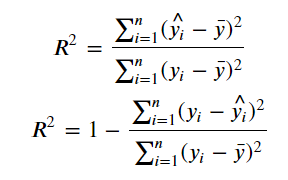

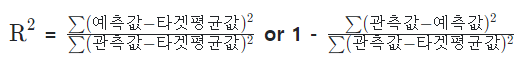
3. 기본 예제
3.1 import
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression # 회귀 문제를 위한 dummy dataset 생성
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LinearRegression # 선형 회귀 모델
3.2 Dataset 생성
- make_xxxxx() 함수
- 머신러닝 학습을 위한 dummy dataset 구현 함수
- 필요한 설정을 직접하여 테스트할 수 있는 데이터셋을 생성해준다.
- make_regression(): 회귀 문제를 위한 dummy dataset 생성
- make_classification(): 분류 문제를 위한 dummy dataset 생성
1) 회귀 문제를 위한 dummy dataset 생성
- 우리가 실제 사용하는 데이터는 모집단이 아닌 샘플 이기에 무작위 에러(noise) 를 추가로 더한 수식인 데이터 셋을 만든다.
X, y = make_regression(n_samples=1000, # 표본의 갯수
n_features=1, # feature의 수
# n_targets = 1, # target의 수 def = 1
n_informative=1, # feature 중 실제 target과 상관 관계가 있는 수
noise=50, # target 에 더해지는 정규 분포의 표준편차 # 안 하면 거의 직선 나옴
random_state=0)
2) dataset shape 확인
X.shape, y.shape((1000, 1), (1000,))
3) dataset scatter 확인
plt.scatter(X, y)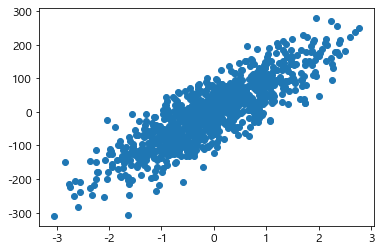
4) dataset 평균, 최소값, 최대값, 중앙값 확인
np.mean(y), np.min(y), np.max(y), np.median(y)(-2.4124246930110305,
-309.93372019710404,
278.9216433229993,
-0.8565443356377808)
3.3 모델 생성, 학습, 추론
lr = LinearRegression() # 선형 회귀 모델 객체
lr.fit(X, y) # 학습
pred = lr.predict(X) # 학습 데이터 셋으로 예측
3.4 평가
mse = mean_squared_error(y, pred)
r2 = r2_score(y, pred)
print("MSE : ", mse)
print("RMSE : ", np.sqrt(mse))
print('R^2 : ', r2)MSE : 2461.0377337239934
RMSE : 49.60884733315211
R^2 : 0.7264007364619969
3.5 교차검증 (cross validation)
- 회귀 모델 기본 평가지표 R square 검증 => scoring = 'r2'
# 데이터 셋을 5개로 나누고 5번 반복하면서 평가하는 작업을 처리
score = cross_val_score(lr, X, y, cv=5)
print("cv별 R2:", score) # 각 반복마다의 평가점수를 배열로 반환
print("평균 R2: ", np.mean(score))cv별 R2: [0.75601278 0.698025 0.72635497 0.72045804 0.72727316]
평균 R2: 0.7256247907760487
- 회귀 모델 mse 검증 = > scoring = 'neg_mean_squared_error'
score = cross_val_score(lr, X, y, scoring='neg_mean_squared_error', cv=5)
print("mse:", score*-1)
print("mse평균: ", np.mean(score)*-1)mse: [2010.85262268 2838.55092577 2644.84308496 2556.21216438 2309.34464992]
mse평균: 2471.9606895426596
3.6 모델이 찾은 계수(coef, 가중치-weigth) 와 절편(intercept, 편향-bias) 조회
- LinearRegression 모델이 학습해서 찾는 파라미터 제공 attribute
이 값으로 우린 선을 추정할 수 있다.
- coef_: Feature에 곱하는 가중치
- intercept_: 모든 Feature가 0일때 예측값
lr.fit(X, y)
print("coef:", lr.coef_, "intercept:",lr.intercept_) # 직선의 기울기와 y절편coef: [81.89512864] intercept: 1.2938791888157457
3.7 X, y 추론 결과 시각화
plt.figure(figsize=(8,6))
plt.scatter(X, y)
# y_hat = X*lr.coef_ + lr.intercept_ # 학습으로 찾은 파라미터
y_hat = lr.predict(X) # 추정한 선
plt.plot(X, y_hat, color='red')
plt.show()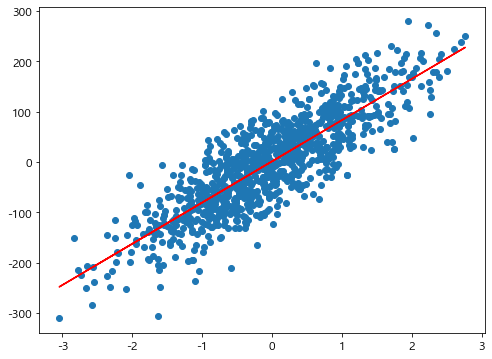
** 회귀에 대한 평가 지표를 출력하는 함수
def print_regression_metrics(y, y_pred, title=None):
"""
회귀에대한 평가지표를 출력하는 함수
mse, rmse, r2 값을 계산해서 출력
[Parameter]
y: ndarray - 정답 배열
y_pred: ndarray - 모델이 예측한 배열
title: str - 제목
"""
mse = mean_squared_error(y, y_pred)
rmse = mean_squared_error(y, y_pred, squared=False)
r2 = r2_score(y, y_pred)
if title:
print(title)
print(f"MSE:{mse}, RMSE:{rmse}, R Square:{r2}")
'AI_STUDY > 머신러닝' 카테고리의 다른 글
| 머신러닝 _ 13_02 선형회귀 _ 다항회귀 (0) | 2022.07.14 |
|---|---|
| 머신러닝 _ 13_01 선형회귀 모델 개요 (0) | 2022.07.14 |
| 머신러닝 _ 08_지도학습_SVM (0) | 2022.07.14 |
| 머신러닝 _ 07_ 지도학습 _ 최근접이웃 (0) | 2022.07.10 |
| 머신러닝 _ 06_2_파이프라인 (0) | 2022.07.09 |




