ㅅㅇ
머신러닝 _ 08_지도학습_SVM 본문
플레이데이터 빅데이터캠프 공부 내용 _ 7/5
머신러닝 _ 08_지도학습_SVM
1. Support Vector Machine (SVM)
: 하나의 분류 그룹을 다른 그룹과 분리하는 최적의 경계를 찾아내는 알고리즘
- 딥러닝 이전에 분류에서 뛰어난 성능으로 많이 사용되었던 분류 모델. 특히 이미지 분류 모델
- 중간 크기의 데이터셋과 특성이 (Feature) 많은 복잡한 데이터셋에서 성능이 좋은 것으로 알려져있다.
1.1 모델 파라미터
- 우리는 선형 SVM 과 비선형 SVM 을 배울 것이다. 파라미터에 대해서 아래에서 자세히 설명.
(1) 선형 모델
- Kernel : 결정 경계 형태 결정
= linear
- C
(2) 비선형 모델 - rbf
- Kernel : 결정 경계 형태 결정
= rbf (기본값)
- C
- gamma
2. 선형(Linear) SVM
2.1 선형 SVM 의 목표
- 선 (1)과 (2)중 어떤 선이 최적의 분류 선일까?
= > 새로운 데이터들이 아래와 같이 분포할 때, 경계선 근처에 있는 모호한 애들은 오류를 날 가능성이 크다.
패턴을 확실하게 구분하기 위해서 margin이 넓은 선을 찾는 것이 SVM 모델의 목표이다.

== > 목표 : support vector간의 가장 넓은 margin을 가지는 초평면(결정경계)를 찾는다.
: margin이 넓은 결정경계를 만드는 함수를 찾는 것.

- 초평면
: 데이터가 존재하는 공간보다 1차원 낮은 부분공간
- n차원의 초평면은 n-1차원
- 공간을 나누기 위해 초평면을 사용한다.
- 1차원-점, 2차원-선, 3차원-평면, 4차원이상 초평면
- Support Vector
: 경계를 찾아내는데 기준이 되는 데이터포인트.
초평면(결정경계)에 가장 가까이 있는 vector(데이터포인트)를 말한다.
- margin
: 두 support vector간의 너비
2.2 규제 - Hard Margin, Soft Margin
- SVM은 데이터 포인트들을 잘 분리하면서 Margin 의 크기를 최대화하는 것이 목적이다.
- Margin의 최대화에 가장 문제가 되는 것이 ' Outlier(이상치) ' 들이다.
= > Train set의 Outlier들은 Margin을 매우 좁게 하여 Overfitting에 주 원인이 된다.
- ' Margine을 나눌 때 Outlier을 얼마나 무시할 것인지' 에 따라 Hard margin과 soft margin으로 나뉜다.
= > 하이퍼파라미터 C 로 결정 !!
1) Hard Margin
- Outlier들을 무시하지 않고 Support Vector를 찾는다.
그래서 Support Vector와 결정 경계 사이의 거리 즉 Margin이 매우 좁아 질 수 있다.
학습시 이렇게 개별 데이터포인트들을 다 놓치지 않으려는 기준으로 결정 경계를 정해버리면
overfitting 문제가 발생할 수 있다.
2) Soft Margin
- 일부 Outlier들을 무시하고 Support Vector를 찾는다.
즉 Outlier들이 Margin 안에 어느정도 포함되도록 기준을 잡는다.
그래서 Support Vector와 결정 경계 사이 즉 Margin의 거리가 넓어진다.
무시비율이 너무 커지면 underfitting 문제가 발생할 수 있다.
2.3 선형SVM _ 하이퍼파라미터 C
: Outlier 를 무시하는 비율을 설정하여 마진을 변경하는 하이퍼파라미터 (기본값 1)
- 노이즈가 있는 데이터나 선형적으로 분리 되지 않는 경우 하이퍼파라미터인 C값을 조정해 마진을 변경한다.
1) C 파라미터값을 크게주면 제약조건을 강하게 한다. = > Hard Margin
- 마진폭이 좁아져 마진 오류가 작아지나, Overfitting이 일어날 가능성이 크다. => C를 줄여준다.
2) C 파라미터값을 작게 주면 제약조건을 약하게 한다. = > Soft Margin
- 마진폭이 넓어져 마진 오류가 커진다.
- 훈련데이터에서는 성능이 안 좋아지나,
일반화(generalization)되어 테스트 데이터의 성능이 올라간다.
그러나 underfitting 이 날 가능성이 있다. => C를 늘려준다.
2.4 선형 SVM 예제
# from sklearn.datasets import load_breast_cancer
1) 데이터 로딩, 셋 나누기, 전처리
import numpy as np
import pandas as pd
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC # svc 모델
from sklearn.metrics import accuracy_score
X, y = load_breast_cancer(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=0)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
2) 모델 생성, 학습, 예측, 평가
: 규제 파라미터인 C 값을 변경하면서 accuracy 성능 확인
c_params = [0.0001, 0.001, 0.01, 0.1, 1, 10,100]
train_acc_list = []
test_acc_list = []
for c in c_params:
svc = SVC(kernel='linear', C=c, random_state=0) # kernel : 선형모델, c 하이퍼파라미터
svc.fit(X_train_scaled, y_train)
pred_train = svc.predict(X_train_scaled)
pred_test = svc.predict(X_test_scaled)
train_acc_list.append(accuracy_score(y_train, pred_train))
test_acc_list.append(accuracy_score(y_test, pred_test))
3) 평가 확인 (데이퍼프레임, plot)
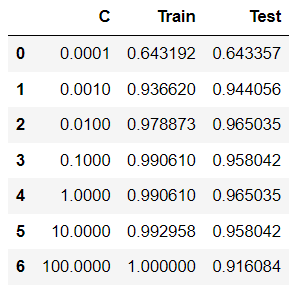
result_df = pd.DataFrame({
'C':c_params,
'Train':train_acc_list,
'Test':test_acc_list
})
result_dfimport matplotlib.pyplot as plt
c = np.log10(np.array(c_params)) # 상용로그로
plt.figure(figsize=(8,6))
plt.plot(c, train_acc_list, marker='o', label="Train")
plt.plot(c, test_acc_list, marker='x', label='Test')
plt.ylim(0.9, 1.1)
plt.legend()
plt.show()
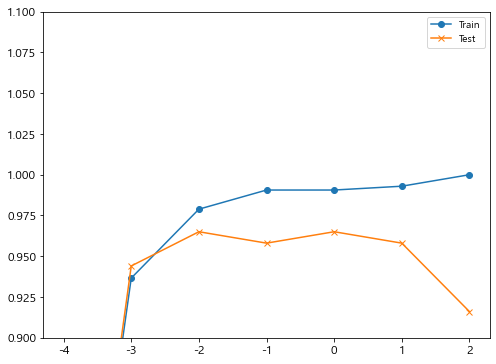
- c = 0.0001 에서 train set 과 test set 모두 성능이 좋지 않다. 너무 단순화된 모델로 학습된 underfitting 이 일어났다.
- c 가 커짐에 따라 모델의 복잡해지며, train set 성능은 올라간다.
c = 100 까지 키웠을 때 train set = 1.00 인 것을 보았을 때 overfitting 이 일어난 것을 알 수 있다.
- val set 은 c 를 키우면서 성능이 올라가다가 overfitting 의 영향으로 다시 떨어지는 것 을 볼 수 있다.
= > val data set 의 성능이 어느정도 높으면서도
train data set 성능과 차이가 적은 0.01 이 최적의 하이퍼파라미터라 생각된다.
3. 커널 SVM : 비선형 데이터 셋에 SVM 적용
선형이 아닌 비선형 데이터 셋에서는 어떻게 분리를 할 수 있을까? == > 커널 트릭
3.1 커널의 원리
: 데이터를 더 높은 차원으로 이동시켜 고차원 공간에서 데이터를 분류하고자 함이다.
- 아래와 같이 선형으로 분리 되지 않는 데이터 셋으로 설명하고자 한다.
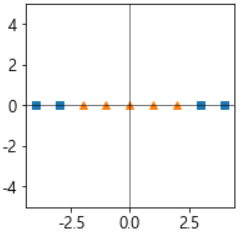
- 이때, 커널의 원리에 따라 다항식 특성을 추가하여 차원을 늘려 선형 분리가 되도록 변환한다.

- 원래 공간으로 변환시킨다.
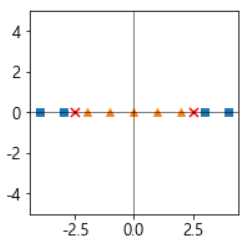
그러나, 차원을 늘리는 경우의 문제가 있다.
- 다항식 특성을 추가하는 방법은
낮은 차수의 다항식은 데이터의 패턴을 잘 표현하지 못해 과소적합이,
너무 높은 차수의 다항식은 과대적합과 모델을 느리게 하는 문제가 있다.
3.2 커널 트릭
- 다항식을 만들기 위한 특성을 추가하지 않으면서
수학적 기교를 적용해 다항식 특성을 추가한 것과 같은 결과를 얻을 수 있는 방식
- 커널 트릭을 위한 다양한 함수가 있는데 이중 "방사 기저 함수" 가 제일 많이 사용된다.
3.3 방사기저 함수 (radial base function - RBF)
- 커널 서포트 벡터 머신의 기본 커널 함수
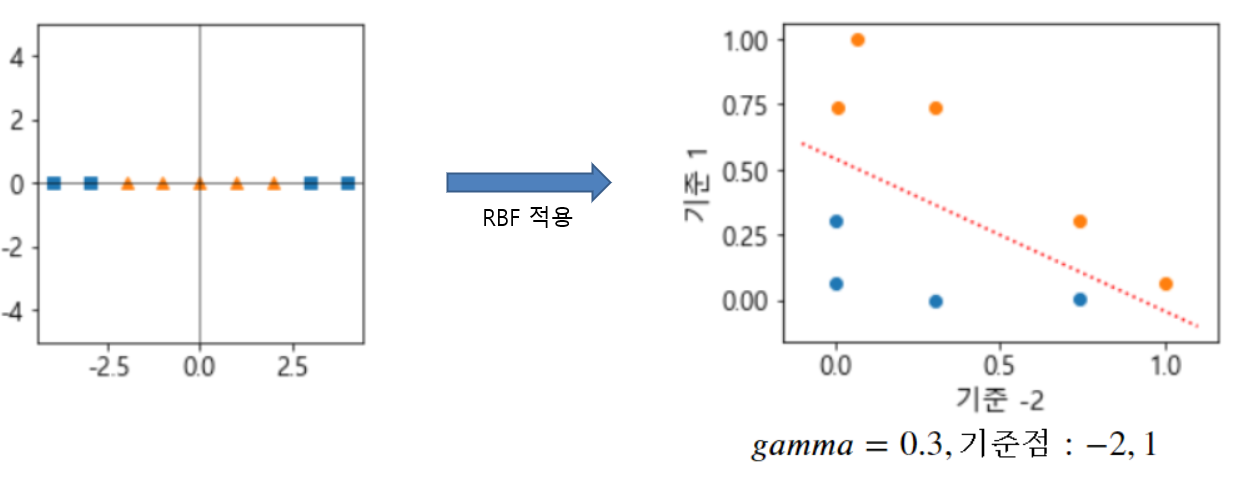
- 기준점들이 되는 위치를 지정하고 각 샘플이 그 기준점들과 얼마나 떨어졌는 지를 계산한다. => 유사도(거리)
- 기준점 별 유사도 계산한 값은 원래 값보다 차원이 커지고 선형적으로 구분될 가능성이 커진다.
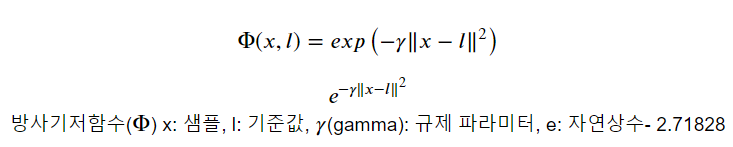
3.4 rbf(radial basis function) 하이퍼파라미터
(1) C : 오차 허용기준.
- 작은 값일 수록 많이 허용한다. (모델을 단순화 시킨다.) 과소적합이 날 가능성이 높아진다.
- 큰 값일 수록 복잡한 모델이 되어 과대적합이 날 가능성이 높아진다.
= > 과대적합일 경우 값을 감소시키고, 과소적합일 경우 값을 증가 시킨다.
(2) gamma : 방사기저함수의 𝛾 로 규제의 역할을 함.
- 큰 값일 수록 과대적합이 날 가능성이 높아진다.
- 모델이 과대적합일 경우 값을 감소시키고, 과소적합일 경우 값을 증가시킨다.
3.5 rbf 의 하이퍼파라미터 Gamma 변경에 따른 성능 변화 확인
gamma_param = [0.0001, 0.001, 0.01, 0.1, 1, 10, 100]
train_acc_list = []
test_acc_list = []
for gamma in gamma_param:
svc = SVC(kernel='rbf', # default가 rbf->생략가능
C=1,
gamma=gamma,
random_state=0)
svc.fit(X_train_scaled, y_train)
pred_train = svc.predict(X_train_scaled)
pred_test = svc.predict(X_test_scaled)
train_acc_list.append(accuracy_score(y_train, pred_train))
test_acc_list.append(accuracy_score(y_test, pred_test))
- 결과 데이터프레임으로 확인
=> gamma = 0.01 에서 train 과 test 성능의 차이도 안 나며, test set 성능 자체도 좋다.
result_df = pd.DataFrame({
'gamma':gamma_param,
'train':train_acc_list,
'test':test_acc_list
})
result_df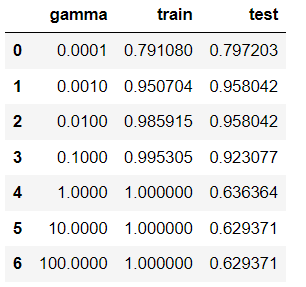
- best model을 이용해 Test set 최종평가
gamma = 0.01 에서 학습, X_test_scaled 예측 후 ROC AUC score, AP score 확인
- 평가함수의 매개변수: (정답, Positive의 확률) ==> model.predict_proba(X)[:, 1]
svc = SVC(C=1, gamma=0.01, random_state=0, probability=True) #probability=True로 주고 객체를 생생해야 predict_proba()를 사용할 수 있다.
svc.fit(X_train_scaled, y_train)SVC(C=1, gamma=0.01, probability=True, random_state=0)
prob_test = svc.predict_proba(X_test_scaled)
from sklearn.metrics import roc_auc_score, average_precision_score
roc_auc_score(y_test, prob_test[:, 1]), average_precision_score(y_test, prob_test[:, 1])(0.9924528301886792, 0.9955101133947021)3.6 GridSearch로 최적의 조합찾기
1) GridSearchCV 생성 및 학습
param = {
'kernel':['rbf', 'linear'],
'C':[0.001, 0.01, 0.1, 1, 10, 100],
'gamma':[0.001, 0.01, 0.1, 1, 10] #linear는 의미가 없는 hyper parameter
}
svc = SVC(random_state=0, probability=True)
gs_svc = GridSearchCV(svc,
param_grid=param,
scoring='accuracy',
cv=4,
n_jobs=-1)
gs_svc.fit(X_train_scaled, y_train)GridSearchCV(cv=4, estimator=SVC(probability=True, random_state=0), n_jobs=-1,
param_grid={'C': [0.001, 0.01, 0.1, 1, 10, 100],
'gamma': [0.001, 0.01, 0.1, 1, 10],
'kernel': ['rbf', 'linear']},
scoring='accuracy')
2) GridSearchCV 에서 하이퍼파리미터 변화에 따른 accuracy 평가 결과확인
- 가장 좋은 성능을 낸 parameter 조합
gs_svc.best_params_{'C': 100, 'gamma': 0.001, 'kernel': 'rbf'}
- 가장 좋은 accuracy 점수
gs_svc.best_score_0.985959266443308
- 파라미터 조합별 평가 결과를 데이터 프레임으로
import pandas as pd
df = pd.DataFrame(gs_svc.cv_results_)
df.sort_values('rank_test_score').head(10)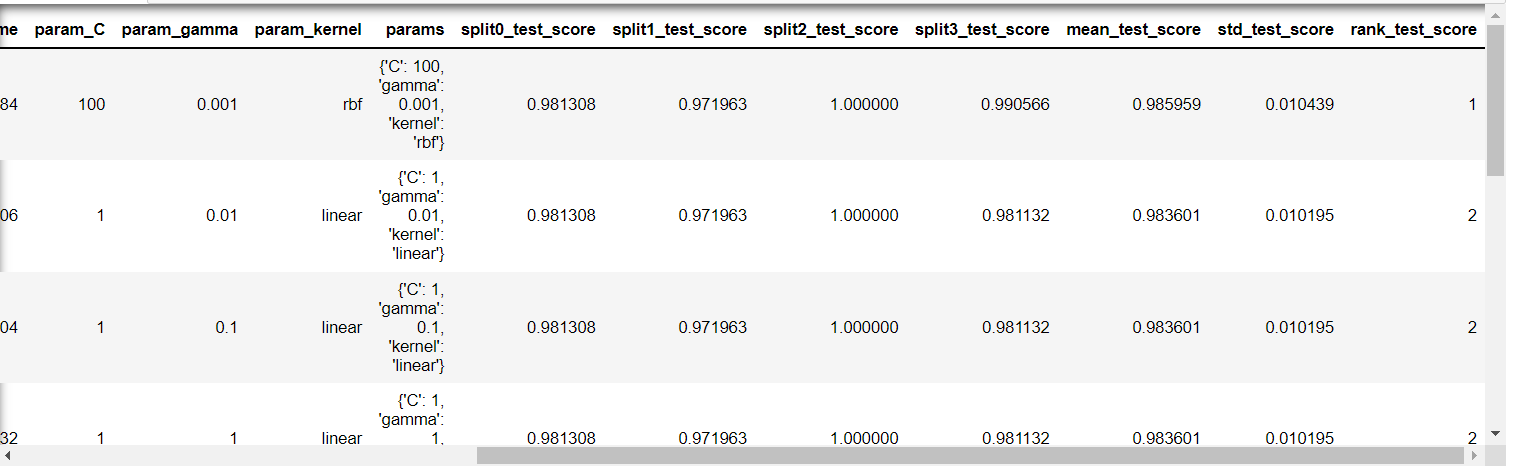
3) Train/Test set 예측 및 accuracy 평가
pred_train = gs_svc.predict(X_train_scaled)
pred_test = gs_svc.predict(X_test_scaled)
print(accuracy_score(y_train, pred_train), accuracy_score(y_test, pred_test))0.9906103286384976 0.958041958041958
4) confusion matrix : 모델이 예측한 결과와 정답간의 개수를 표로 제공
# axis =0 : 예측 label 0,1
# axis=1 : 정답 label 0,1
# value : 예측한 갯수
- label 0 : 48개는 0 으로 예측, 5개는 1로 예측
- label 1 : 1개는 0 으로 예측, 89개는 1로 예측
from sklearn.metrics import classification_report, confusion_matrix
# confusion matrix
confusion_matrix(y_test, pred_test)array([[48, 5],
[ 1, 89]], dtype=int64)
- classification_report 분류 평가지표 확인
정확도(Accuracy), 정밀도(Precision), 재현률(Recall), F1점수(F1 Score) 확인
print(classification_report(y_test, pred_test)) precision recall f1-score support
0 0.98 0.91 0.94 53
1 0.95 0.99 0.97 90
accuracy 0.96 143
macro avg 0.96 0.95 0.95 143
weighted avg 0.96 0.96 0.96 143
print(classification_report(y_train, pred_train)) precision recall f1-score support
0 0.99 0.98 0.99 159
1 0.99 1.00 0.99 267
accuracy 0.99 426
macro avg 0.99 0.99 0.99 426
weighted avg 0.99 0.99 0.99 426'AI_STUDY > 머신러닝' 카테고리의 다른 글
| 머신러닝 _ 13_01 선형회귀 모델 개요 (0) | 2022.07.14 |
|---|---|
| 머신러닝 _ 12_회귀모델개요_평가지표 (0) | 2022.07.14 |
| 머신러닝 _ 07_ 지도학습 _ 최근접이웃 (0) | 2022.07.10 |
| 머신러닝 _ 06_2_파이프라인 (0) | 2022.07.09 |
| 머신러닝 _ 06_1_과적합 일반화와 그리드 서치 (0) | 2022.07.06 |



