ㅅㅇ
딥러닝 _03_1_DNN (Deep Neural Network) 신경망 구조 본문
플레이데이터 빅데이터캠프 공부 내용 _ 7/12
딥러닝 _03_DNN (Deep Neural Network) 신경망 구조 (1)
1. Neural Network 신경망 : 가장 기본적인 Deep Learning 모델 구조
MSP(Multi Layer Perceptron)
Multi Layer = Deep, Neural Network = Perceptron
2. 신경망 구성요소
- 층(Layer) : Network를 구성하는 Layer(층)
= > 각각의 layer 는 parameter(모델 학습할 대상 - 학습을 통해 찾아야 파라미터) 를 가지고 있다.
- feature 과 label 를 가지고
둘의 관계를 말하는 함수를 찾기위해 각 layer의 parameter 를 찾아 식을 완성하는 게 학습에서 하는 '예측'이다.
이때 파라미터는 'loss 함수 연산' 을 통해
예측과 정답 간의 오차가 가장 적은 최적의 값을 찾아 파라미터를 업데이트한다. = > '최적화'
- 학습
- 모델( 구조 - 우리가 정의(하이퍼파라미터) ) : 예측
- 손실( 오차 ) 계산 : Loss 함수(컴파일 시 설정)
- 최적화( 파라미터 - 가중치 업데이트) : Optimizer (옵티마이저 - 컴파일시 설정)
(1) 모델 : 예측하는 함수
- 기본식을 가지고 조정값 설정
= > 우리가 정의하는 하이퍼 파라미터
(2) 손실함수(loss function) : 가중치를 어떻게 업데이트할 지 예측결과와 Ground truth(실제정답) 사이의 차이를 정의
(3) optimizer : 가중치(학습 파라미터)를 업데이트하여 모델의 성능을 최적화 = > 경사하강법
- 학습을 할 때 parameter (가중치) 가 틀렸으니 오차가 발생한 것이다.
손실함수로 오차를 구해 오차가 최소화되도록 가중치를 업데이트를 한다.
- 학습에서 위 처리들이 필요하기에
모델 생성에서 layer들을 만들어주고,
컴파일 단계를 통해 손실함수와 옵티마이저를 셋팅해준 것이다.
3. Train(학습) 프로세스

- 데이터가 들어가면, 1) 예측- 모델 2) 오차(loss 손실) -loss함수 3) parameter update-옵티마이저
- 60000개 중에 100개가 input 으로 들어간다.
각각의 모델 layer 처리로 예측을 하여 예측값이 나오면 정답과 비교를 해 loss 함수로 오차를 구한다.
100개 데이터에 대한 100개의 오차가 나오는데 이를 평균을 낸다.
- 평균 오차를 0으로 만들기 위해 옵티마이저가 각각의 모델들의 parameter(가중치) 를 update 한다. (=>1step)
- 그리고 그다음 100개로 동일한 단계를 거친다(2step). 또 100개로 처리한다.(3step) ...
60000개 데이터 다하면 1epoch
== > 60000개를 100개씩 끊어서 학습하는데, 1epoch 당 600 step
== > 600 개의 parameter update를 하는 것이다. => 많이 할 수록 train 성능 올라감!
- 10epoch : 이 처리들을 10번 하라는 것
4. 유닛/노드/뉴런 (Unit, Node, Neuron)
- logistic regression 모델 하나를 뜻한다. (머신러닝에서 logistic regression 설명함.)
- Tensor를 입력받아 처리후 tensor를 출력하는 데이터 처리 모듈 : Input - > Output
- 각 입력 값에 각 Weight(가중치)를 곱하고 bias(편향)을 더한 결과 𝕨𝑇𝕩+𝑏 를
Activation 함수 𝜎(𝑧) 에 넣어 최종 결과를 출력하는 계산을 처리한다


5. 각 레이어/층(layer) 설명
레이어/층(Layer) : unit 을 모아놓아 한 단계를 표현한 것.
- 대부분 Layer들은 학습을 통해 최적화할 Paramter를 가짐
- Dropout, Pooling Layer와 같이 Parameter가 없는 layer도 있다.
- Layer들의 연결한 것을 Network 라고 한다.
- 딥러닝은 Layer들을 깊게 쌓은 것을 말한다. (여러 Layer들을 연결한 것)
1) Input Layer(입력층)
- 입력값들을 받아 Hidden Layer에 전달하는 노드들로 구성된 Layer.
- 역할 : 입력 데이터의 shape을 설정
- 학습과 관련된 처리를 하는 layer가 아니라 그저 입력을 받아 전달하는데, 이 layer는 왜 필요할까?
한 유닛에 여러 feautre 가 input 으로 들어가면,
하나의 feature 에 하나의 weight 를 구한다.
즉, 각각의 feature에 곱해질 가중치가 준비되야 하는 것이다.
이렇게, feature (shape) Input 에 맞춰 가중치 W 값들을 랜덤하게 준비되어야 하므로 Input layer 가 필요한 것.
- koras.layers.InputLayer((28,28))
- data 의 Feature shape 을 알려주고 있다.
(28,28) => 2차원 배열, 0 축:28, 1축 :28 값으로 구성되어 있다고 알려줌.
train_image(X).shape = (60000, 28,28)
: 60000는 데이터 개수, (28,28) 는 1개 데이터의 shape 라는 뜻이다.
2) Output Layer(출력층)
- 모델의 최종 예측결과를 출력하는 노드들로 구성된 Layer
- model.add(keras.layers.Dense(10, activation='softmax'))
- unit 개수 : 출력 결과의 개수. 정답 클래스 개수
- ex) 현 예제 데이터셋가 다중 분류. class 0 ~ 9 총 10개이라면?
=> 각 클래스 별 확률이 출력되도록 unit 수를 설정한다.
(10개 클래스 별 확률이 출력되도록 하기 위해서 unit 수를 10 으로 설정.)
- activation : 활성 함수의 종류를 지정
- ex) 'softmax' : 활성함수(activation function)의 종류를 softmax 함수로 지정.
- 입력과 출력은 데이터 셋, 학습 등에 의해 거의 정해져 있지만, 딥러닝의 Hidden Layer 는 art 개발자가 정한다.
3) Hidden Layer(은닉층)
- Input Layer와 Output Layer사이에 존재하는 Layer.
- 특성 추출(Feature Extraction), 추론하는 역할 을 담당.
- Layer 개수, Layer 당 unit의 개수, 각 Layer 에 어떤 활성함수 를 사용할 것인지는 Hyper parameter 이다.
(Art - 공식으로 정해진 것이 아니라 경험이나 테스트를 통해 찾아야 한다.)
- 목적, 구현 방식에 따라 다양한 종류의 Layer 들
2), 3), 4) 가 특성을 추출하는 layer 이고, 추출한 특성으로 추론하는 것이 Fully Connected Layer 이다.
1) Fully Connected Layer (Dense layer)
- 추론 단계에서 주로 사용
2) Convolution Layer
- 이미지 Feature extraction으로 주로 사용
3) Recurrent Layer
- Sequential(순차) 데이터의 Feature extraction으로 주로 사용
- ex. 시계열 데이터(시간의 흐름이 중요한 feature)
4) Embedding Layer
- Text 데이터의 Feature extraction으로 주로 사용
6. 모델 (Network)
: Layer를 연결한 것이 Deep learning 모델이다.
- 이전 레이어의 출력을 input으로 받아 처리 후 output으로 출력하는 레이어들을 연결한다.
- 적절한 network 구조(architecture)를 찾는 것은 공학적이기 보다는 경험적(Art)접근이 필요하다.
- 딥러닝은 쌓는다고(수직구조) 표현을 한다.
- Bottom Layer: Input Layer(입력층)에 가까이 있는 Layer들.
- Top layer: Output Layer(출력층)에 가까이 있는 Layer들
(이를 나중에 arg 으로 쓸 때가 있다.)
- 왜 여러 개의 layer 를 쌓아 처리하냐 ? 각자의 역할이 다르기 때문에.
- input : 입력값을 받아서 다음으로 전달. 입력값의 shape 변수를 지정하는 역할
- ouput : 최종추론 결과를 출력해주는 역할
- hidden : bottom 쪽 - feature 추출, top 쪽 - 추론하는 역할
- 추출, 추론 하는 애들 몇 개 만들지는 우리가 정하는 것.art

7. 활성함수 (Activation Function)
: 각 유닛이 입력과 Weight 간에 가중합을 구한 뒤 출력결과를 만들기 위해 거치는 함수
- 같은 층(layer)의 모든 유닛들은 같은 활성 함수를 가진다.
- 활성함수는 비선형함수
- 분배법칙이 되지 않게 비선형 형태가 되어야 한다.
그래야 각각의 다른 처리가 된다. 이를 내부적으로 처리하는 게 활성함수라 한다.
- 은닉층 (Hidden Layer)의 경우 비선형성을 주어 각 Layer가 처리하는 일을 분리하는 것을 목적으로 한다.
- 비선형함수를 사용하지 않으면 Layer들을 여러개 추가하는 의미가 없어진다.
- ReLU 함수를 주로 사용한다. ( relu 또는 relu의 변형(ru 붙은 애들)
- 출력 레이어의 경우 출력하려는 문제에 맞춰 활성함수를 결정
- 다중 : softmax
- 이진 : sigmoid
- 회귀 : None => 기본적으로 안 쓰지만, 정답의 shape에 따라 변경할 수 있다.
- 회귀 출력층은 보통, 결과값 (추론해야할 연속형 값) 을 만드는 게 목적이기에 그냥 쭉 통과시킨다.
- 예외 ex ) 경우적으로 써야 할 때가 출력값이 어떤 범위로 출력되어야 할 때
가끔 예측해야하는 값이 y가 0 ~ 1 실수라면, sigmoid 함수가 필요하다.
또, -1 ~ 1 값으로 정규화해야 한다면, 이때 tach 함수를 쓴다.
7.1 주요 활성함수
1. Sigmoid (logistic function)


- 출력값의 범위 : 0<sigmoid(z)<1
- 한계
- 초기 딥러닝의 hidden layer(은닉층)의 activation function(활성함수)로 많이 사용 되었다.
- 층을 깊게 쌓을 경우 기울기 소실(Gradient Vanishing) 문제를 발생시켜
parameter 학습이 안되는 문제 로 성능 개선이 되지 않는다.
- 함수값의 중심이 0이 아니어서 학습이 느려지는 단점이 있다.
- X의 값이 0일때 0.5를 반환한다.
- 현재, Binary classification(이진 분류)를 위한 네트워크의 Output layer(출력층)의 활성함수로 사용된다.
- 모델이 positive(1)의 확률을 출력결과로 추론하도록 할 경우 사용. (unit개수 1, activation함수 sigmoid)
- 위와 같은 한계때문에 hidden layer(은닉층)의 activation function(활성함수)로는 잘 사용되지 않는다.
★기울기 소실(Gradient Vanishing) 문제란 ?
: 최적화 과정에서 gradient가 0이 되어서 Bottom Layer의 가중치들이 학습이 안되는 현상
문제의 원인은 활성화 함수로 사용한 sigmoid 함수의 특성 때문이다.
sigmoid 함수를 미분한 함수의 그래프를 보면 기울기의 최대가 0.25이고 양 끝은 0에 수렴하는 것을 볼 수 있다.
즉, 0 ~ 0.25 사이의 값을 가진다.
딥러닝의 최적화 과정에서는 역전파로 bottom layer 으로 가까이 가면서
sigmoid 함수의 미분을 연쇄적 곱하는데,
기울기가 1보다 작으므로 곱할수록 값은 점점 작아진다.
만약, layer가 아주 많다면, bottom layer 로 가까이 갈수록
기울기의 값은 거의 0 에 가깝게 작아져서 가중치의 변화는 거의 없게 되고 loss 또한 더 이상 줄어들지 않게 된다.
즉, update 되야 하는 가중치들이 더이상 최적화 되지 않는 것이다.
이 문제를 해결한 함수가 ReLU 함수이다.
2. Hyperbolic tangent


- 출력값의 범위 : -1 < tanh(z) < 1
- Output이 0을 중심으로 분포하므로 sigmoid보다 학습에 효율적이다.
- 시그모이드 문제 해결하려고 나왔는데, 여전히 기울기 소실(Gradient Vanishing) 문제를 발생시킨다.
3. ReLU(Rectified Linear Unit)


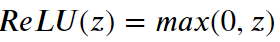
- 입력값이 0 보다 작으면 0
0 보다 크면 입력값 그대로 내보낸다.
- 기울기 소실(Gradient Vanishing) 문제를 어느정도 해결
= > Hidden layer 가장 많이 사용되는 활성화 함수
- 0에서 미분이 되지 않는다.
- 출력값은 0 또는 양수이고, 기울기 또한 0 또는 1인 양수 이다. (최적의 가중치를 찾는 지그재그 현상이 발생할 것)
- 입력값이 음수라면 기울기가 0 이 되어 가중치 update가 되지 않을 것이다.
=> 0 이하의 값(z <= 0)들에 대해 뉴런이 죽는 단점이 있다. (Dying ReLU)
- 이러한 단점을 보완하는 다양한 형태의 ReLU 함수들을 연구해왔다.
4. Leaky ReLU


- ReLU의 Dying ReLU 현상을 해결하기 위해 나온 함수
- 가 0보다 크면
0보다 같거나 작으면 𝛼 를 반환한다. - - - alpah (0 ~ 1 사이 실수) 를 곱해 반환
= > 음수 z를 0으로 반환하지 않는다.
가 음수인 영역의 값에 대해 미분값이 0이 되지 않는다는 점을 제외하면 ReLU의 특성을 동일하게 갖는다.
5. Softmax

- Multi-class classification(다중 분류)를 위한 네트워크의 Output layer(출력층)의 활성함수로 주로 사용된다.
- 은닉층의 활성함수로 사용하지 않는다.
- Layer의 unit들의 출력 값들을 정규화 하여 각 class에 대한 확률값으로 변환해주는 함수
- exp해당값/exp값의합 (큰 값 나오는 애가 큰 확률 나오게)
- 출력노드들의 값은 0 ~ 1사이의 실수로 변환되고 그 값들의 총합은 1이 된다.
- API
[ 활성화 함수 정리 ]

8. 손실함수(Loss function, 비용함수)
: Model이 출력한 예측값(prediction) 𝑦̂ 와 실제 데이터(output) 𝑦 의 차이를 계산하는 함수
- 네트워크 모델을 훈련하는 동안
Loss 함수가 계산한 Loss값(손실)이 최소화 되도록 파라미터(가중치와 편향)을 업데이트한다.
=> 즉 Loss함수는 최적화 시작이 되는 값이다.
- 네트워크 모델이 해결하려는 문제의 종류에 따라 다른 Loss함수를 사용한다.
=> 해결하려는 문제의 종류에 따라 표준적인 Loss function이 있다.
8.1 해결하려는 문제의 종류에 따른 Loss Function
1) Classification (분류)

= = > cross entropy (log loss) 사용
이진분류 공식이나 다중 분류 공식이나 정답에 대한 확률에 log 처리 해준 것이다.
1-1 ) Binary classification (이진 분류)
- 두 개의 클래스를 분류
- 둘 중 하나 (0 또는 1)
- 예) 문장을 입력하여 긍정/부정 구분
- Output Layer의 unit 개수를 1로 하고 activation 함수로 sigmoid를 사용하여 positive(1)의 확률로 예측 결과를 출력하도록 모델을 정의한 경우 loss ='binary_crossentropy'

1-2 ) Multi-class classification (다중 클래스 분류)
- 두 개 이상의 클래스를 분류
- 여러개 중 하나
- 예) 이미지를 0,1,2,...,9로 구분
- loss = 'categorical_crossentropy'

2) Regression (회귀)
- 연속형 값을 예측
- 예) 주가 예측
- Mean squared error를 loss function으로 사용 (오차를 제곱)
- loss = 'mse' 로 지정

9. 평가지표
- 모델의 성능을 평가하는 지표
- 손실함수(Loss Function)와 차이
- 손실함수는 모델을 학습할 때 가중치 업데이트를 위한 오차를 구할 때 사용한다.
- 평가지표 함수는 모델의 성능이 확인하는데 사용한다.
[ ★ 문제별 출력레이어 Activation 함수, Loss 함수 ]

'AI_STUDY > 딥러닝' 카테고리의 다른 글
| 딥러닝 _05_DNN_성능개선 (0) | 2022.07.25 |
|---|---|
| 딥러닝_04_tfdata 파이프라인 (0) | 2022.07.14 |
| 딥러닝 _03_2_DNN (Deep Neural Network) 신경망 구조 _ 최적화 (0) | 2022.07.13 |
| 딥러닝 _02_첫번째 딥러닝- MLP 구현 (0) | 2022.07.12 |
| 딥러닝 _ 01_ 개요 및 Tensorflow 설치 (0) | 2022.07.11 |



