ㅅㅇ
numpy _ 04_2 범용함수(Ufunc, Universal function) 본문
numpy _ 04_2 범용함수(Ufunc, Universal function)
1. 범용함수란
- 벡터화를 지원하는 넘파이 연산 함수들.
- 유니버셜 뜻이 "전체에 영향을 미치는" 이다.
그래서 이 함수는 배열의 원소 전체에 영향을 미치는 기능을 제공하는 함수다.
- 배열의 원소별로 연산 을 처리하는 함수들
- 반복문을 사용해 연산하는 것 보다 유니버셜 함수를 사용하는 것이 속도가 빠르다.
2. 주요 범용함수
2.1 단항 범용함수 (unary ufunc)
- 매개변수로 한개의 배열을 받는다.
- 한 배열내의 원소별로 연산

2.2 이항 범용함수
- 매개변수로 두개의 배열을 받는다.
- 두 배열의 같은 index 원소별로 연산

- 단항 함수 예제
# 단항함수
a = np.array([-3.5, 2.8, 4.2])
# 절대값 반환
print(np.abs(a))
# 제곱근 반환
# print(np.sqrt(a)) # 음수 -3.5의 제곱근 계산이 안되므로 non(결측치)를 반환
print(np.sqrt(np.abs(a))) # 음수일 때, abs()와 함께 쓰면 해결.
# 실수부, 정수부 나눠서 반환
print(np.modf(a))
# np.nan : 결측치를 표현하는 numpy 변수
b = np.array([10, 5, np.nan, 2, np.nan])
# 각 원소별로 결측치 여부를 확인
print(np.isnan(b))
# 결측치의 갯수 # T:1 , F:0 로 변환해서 합계를 구한다.
print(np.sum(np.isnan(b)))[3.5 2.8 4.2]
[1.87082869 1.67332005 2.04939015]
(array([-0.5, 0.8, 0.2]), array([-3., 2., 4.]))
[False False True False True]
2- 이항 함수 예제
# 이항함수
x = np.arange(1,6)
y = np.arange(11,16)
print(np.add(x,y))
print(np.subtract(x,y))
print(np.multiply(x,y))
# 나누기 연산자 x/y
print(np.divide(x,y))
# 몫 연산자 y//x
print(np.floor_divide(y,x))
# 나머지 연산자 x%y
print(np.mod(x,y))
# 같은 index의 값 중 큰 것 / 작은 것 반환
print(np.maximum(x,y), np.minimum(x,y))
# x > y 결과 bool
print(np.greater(x,y))[-10 -10 -10 -10 -10]
[11 24 39 56 75]
[0.09090909 0.16666667 0.23076923 0.28571429 0.33333333]
[11 6 4 3 3]
[1 2 3 4 5]
[11 12 13 14 15] [1 2 3 4 5]
[False False False False False]
2.3 연산결과 출력 지정
- 범용함수의 연산은 계산 결과를 담은 새로운 배열을 생성해서 반환한다.
- - > 연산결과를 특정 배열에 넣을 수 있다.
- 0으로 채워진 (3,3) 구조인 result 배열에 연산 결과를 넣는다.
a = np.arange(11,20).reshape(3,3)
b = np.arange(1,10).reshape(3,3)
result = np.zeros(shape = (3,3)) # 0으로 채워진 (3,3) 구조
np.add(a,b, out = result)
result
3. 누적 연산 함수
3.1 누적연산함수 - reduce()
- 결과가 하나만 남을 때 까지 해당 연산을 배열의 모든 요소에 반복 해서 적용
- 구문
- np.이항범용함수이름.reduce(배열, axis=0)
- 처리결과의 축의개수(rank)는 하나 줄어 든다.
- 1차원 -> 스칼라
- 2차원 - 1차원
- axis 0 방향으로 연산 또는 axis 1 방향으로 연산
- 3차원 - 2차원
- n 차원 - n-1차원
1) 예제 : 1차원 배열 = > 스칼라
x = np.arange(1,11) # [ 1 2 3 4 5 6 7 8 9 10]
print(x)
# 누적합계
r = np.add.reduce(x)
print(r)
# 누적 제곱 (첫번째 배열을 두번째 배열로 제곱)
r = np.power.reduce(x)
r[ 1 2 3 4 5 6 7 8 9 10]
55
1
2) 예제 : 2차원 배열 => 1차원 배열
x = np.arange(1,16).reshape(3,5)
print(x.shape)
x(3, 5)
array([[ 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10],
[11, 12, 13, 14, 15]])
- axis = 0 (def)
r = np.add.reduce(x) # axis = 0
print(np.shape(r))
r(5,)
array([18, 21, 24, 27, 30])
- axis = 1
r = np.add.reduce(x, axis = 1)
print(np.shape(r))
r(3,)
array([15, 40, 65])
- axis = None : flatten(1차원배열) 후 처리 : 전체 합계
r =np.add.reduce(x, axis = None)
r120
3.2 누적연산함수 - accumulate()
- 배열의 원소들에 해당연산을 누적해 적용
- 처리경과의 축의개수(rank)는 피연산자배열과 동일하다.
- 구문
- np.이항범용함수이름.accumulate(배열, axis=0)
(1) 1차원 배열
x = np.arange(1,11) # array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
np.add.accumulate(x)array([ 1, 3, 6, 10, 15, 21, 28, 36, 45, 55], dtype=int32)
(2) 2차원 배열
x2 = np.arange(1,16).reshape(3,5)
print(x2.shape)
x2(3, 5)
array([[ 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10],
[11, 12, 13, 14, 15]])
- axis = 0 (def)
r = np.add.accumulate(x2) # axis = 0
print(r.shape)
r(3, 5)
array([[ 1, 2, 3, 4, 5],
[ 7, 9, 11, 13, 15],
[18, 21, 24, 27, 30]], dtype=int32)
- axis = 1
r = np.add.accumulate(x2, axis = 1)
print(r.shape)
r(3, 5)
array([[ 1, 3, 6, 10, 15],
[ 6, 13, 21, 30, 40],
[11, 23, 36, 50, 65]], dtype=int32)
- accumulate 는 axis를 None으로 지정할 수 없다.
r = np.add.accumulate(x2, axis = None)
(3) .accumulate .reduce 활용 예제
- 과일별 판매량 조회
axis =0 : 날짜, axis 1: 과일
# 열 : 판매수량 [사과, 배, 귤]
# 행 : 날짜별 판매
amt = [
[10,5,7],
[15,3,10],
[1,23,10],
[10,12,50]
]
amt_arr = np.array(amt)
- 과일별 총 판매량, 날짜별 총 판매량
# 과일별 총 판매량
np.add.reduce(amt_arr)
# 날짜별 총 판매량
np.add.reduce(amt_arr, axis =1)array([36, 43, 77])array([22, 28, 34, 72])
- 날짜별로 총판매량 (과일별, 날짜별 누적판매량)
np.add.accumulate(amt_arr)array([[10, 5, 7],
[25, 8, 17],
[26, 31, 27],
[36, 43, 77]], dtype=int32)
4. 기술통계함수
- 배열 원소를 대상으로 통계 결과를 계산해 주는 함수들
- 구문
1. np.전용함수(배열)
- np.sum(x)
2. 일부는 `배열.전용함수()` 구문 지원
- x.sum()
- 배열의 원소 중 누락된 값(NaN - Not a Number)이 하나라도 있을 경우 연산의 결과는 NaN으로 나온다.
- 안전모드 함수
- 배열내 누락된 값(NaN)을 무시하고 계산
- np.전용함수(배열) 구문만 가능
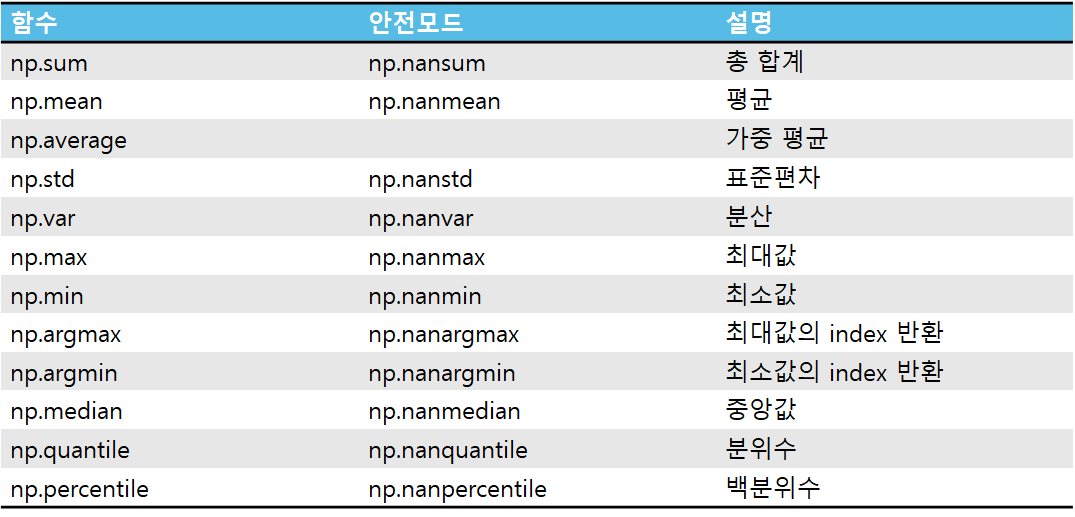
4.1 1차원 배열
(1) 기본 예제
x = np.random.randint(1,100,5)
# max, min
print(np.max(x), np.min(x),sep=',')
print(x.max(), x.min(), sep=',')
# argmax, argmin : 최대/최소값의 index
print(np.argmax(x), np.argmin(x), sep=',')
- 가중평균 : np.average(값, weights= 가중치)
= (값과 가중치의 가중합) / 가중치 총합
= s @ w / w.sum
w = np.array([2,3,1])
s = np.array([100,80,90])
# 산술평균
print(np.mean(s), s.mean())
# 가중평균 : (값과 가중치의 가중합)을 (가중치총합)으로 나눈다.
# s@w/w.sum()
print(np.average(s, weights = w))
- 분위수 : quantile(), percentile()
- > 오름차순 정렬 후 등분했을 때 등분된 위치의 값
- quantile() : q = 분위 0 ~ 1 비율
x = np.random.randint(1, 1000, 11)
# 중앙값/중위수 (오름차순 정렬 후 2등분했을 때 등분된 위치의 값)
np.median(x)
# 4분위수 q = 분위 0 ~ 1 비율
np.quantile(x, q = [0.25, 0.5, 0.75])
# 10분위수
np.quantile(x, q = np.arange(0.1,1.0,0.1))
- percentile() : 백분위 기준으로 분위수를 계산 - q = 0~100 사이 실수
x = np.arange(0,101)
np.percentile(x, q =10), np.quantile(x, q = 0.1)
np.percentile(x, q =[1,2]), np.quantile(x, q = [0.01, 0.02])(10.0, 10.0)(array([1., 2.]), array([1., 2.]))
(2) 예제 : 결측치가 있는 배열
- x.nanmean() 안됨
# 결측치가 있는 배열
x = np.array([10,2,20,7,np.nan,90,100])
# 결측치가 있으면 결과는 nan (결측치를 포함해서 계산하기 때문)
np.sum(x), np.mean(x), np.max(x), np.min(x), np.var(x), np.std(x)
# 안전모드. 결측치 빼고 계산
np.nansum(x), np.nanmean(x), np.nanmax(x), np.nanmax(x)(nan, nan, nan, nan, nan, nan)
(229.0, 38.166666666666664, 100.0, 100.0)
4.2 다차원 배열
- axis(계산 기준 축) 지정해야 함.
= None (def ) : flatten 후 계산. 전체통계
(1) 예제 : 2차원 배열
x = np.arange(24).reshape(4,6)
# 기본값 axis = None 전체기준 통계값(합계)
np.sum(x)
# axis = 0 (합계)
np.sum(x, axis = 0)
# axis =1 (평균)
np.mean(x, axis = 1)
(2) 예제 : 결측치가 있는 배열
- x.nanmean() 안됨
# 결측치가 있는 배열
x = np.arange(12).reshape(3,4)
x = x.astype(np.float32)
x[0,0] = np.nanarray([[nan, 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.]], dtype=float32)
- 결측치 포함하면 결과도 결측치
np.sum(x, axis = 0)
np.sum(x, axis = 1)array([nan, 15., 18., 21.], dtype=float32)array([nan, 22., 38.], dtype=float32)np.nansum(x, axis = 0)
np.nansum(x, axis = 1)array([12., 15., 18., 21.], dtype=float32)array([ 6., 22., 38.], dtype=float32)
np.sum(np.isnan(x))1
- 결측치 갯수 세기 : 0 축 기준 결측치 개수
np.sum(np.isnan(x), axis=0)array([1, 0, 0, 0])
5. boolean indexing 과 sum()/mean()
- sum(boolean indexing) : 특정 조건을 만족하는 원소의 개수
- mean(boolean indexing) : 특정 조건을 만족하는 원소의 비율
1) boolean indexing
# 원소 중 50 이상의 값을 조회
x[x>=50]
# 원소 중 50 이상의 값의 위치(index) 조회
np.where(x>=50)
2) sum(boolean indexing) : 특정 조건을 만족하는 원소의 개수
- boolean 타입 배열 - > 계산(sum) : True=1, False=0
# 월소 중 50 이상의 값의 개수
np.sum(x >=50)
3) mean(boolean indexing) : 특정 조건을 만족하는 원소의 비율
# 원소 중 50 이상의 값의 비율
# true=1 을 다 더해서 / 원소 전체 갯수
np.mean(x>=50)
4) .any : 원소 중 한 개라도 만족하는가?
.all : 모든 원소가 만족하는가?
# 원소 중에 50 이상인 값이 한 개 이상 있는지 여부
np.any(x>=50)
# 모든 원소들이 50이상인지 여부
np.all(x>=50)
'AI_STUDY > Numpy' 카테고리의 다른 글
| numpy _ 04_3 브로드캐스팅 (0) | 2022.06.24 |
|---|---|
| numpy _ 04_1 벡터 연산 (0) | 2022.06.24 |
| numpy _ 02_2 정렬 (0) | 2022.06.24 |
| numpy _ 02_1 배열의 원소 조회 (0) | 2022.06.24 |
| numpy _ 01_2 배열 생성 (0) | 2022.06.23 |


